在哪些情况下无尽的拉格朗日积分有用

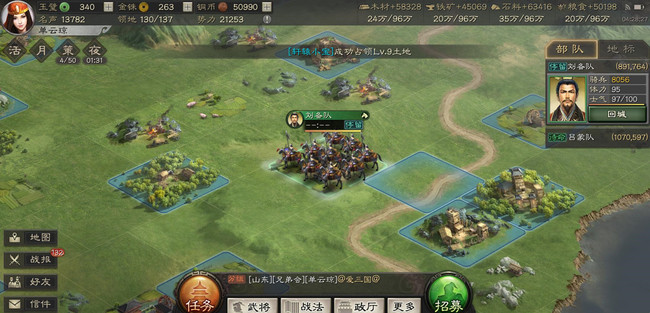
积分系统是玩家获取稀有资源的重要途径之一。积分主要通过赛季评定、协议任务或特定活动获得，其核心用途包括兑换蓝图档案、皮肤、紫币等奖励。蓝图档案能解锁企业版、木星工业等势力的专属舰船蓝图，涵盖护卫舰到航母的全类型舰船，对舰队实力提升有直接影响。皮肤则用于个性化装饰，紫币作为通用货币可购买各类道具。积分兑换的奖励具有长期价值，尤其对非付费玩家而言是弥补资源差距的关键手段。

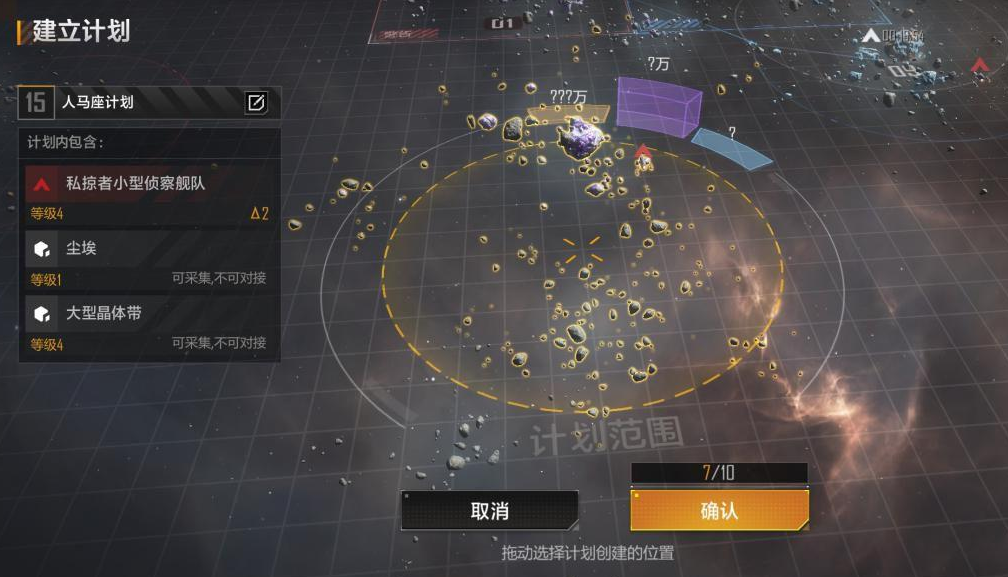
玩家通过完成个人评定目标积累的积分，可在赛季结束后兑换头像、皮肤及势力专属蓝图箱。不同势力蓝图箱需消耗不同积分，例如企业版蓝图档案单价200积分，木星工业蓝图需450紫币兑换。积分兑换策略需根据当前舰队需求调整，优先选择稀缺舰船蓝图或高性价比资源。部分赛季限定奖励仅能通过积分获取，错过兑换周期将无法再次获得，因此合理规划积分使用优先级至关重要。

勘探者协议等特殊玩法中，积分获取效率与勘探目标等级相关。低级资源点如尘埃仅提供1点积分且耗时短，而高级目标如星球勘探需数小时但回报更高。优化勘探队伍配置（如搭配X20与X8舰船）可提升效率，同时需注意勘探点竞争机制——单个点位仅允许一名玩家同时操作。积分积累过程中，需平衡时间成本与收益，避免因过度追求高级目标导致资源浪费。

回归协议与中立者协议提供了额外积分来源。回归玩家通过每日任务可获得上限3000的积分，包括登录、完成势力委托等基础任务。中立协议则允许玩家通过加密通信与私人掠夺者合作，在特定星系购买特洛伊水晶或数据信息，间接提升联盟评估积分。这类协议通常要求玩家保持活跃度，并需熟悉NPC交互规则，例立舰队会主动联系玩家发布任务，及时响应可提高积分获取稳定性。

积分系统的设计强化了游戏的长期目标感。无论是赛季评定、协议任务还是活动奖励，积分获取与消耗均需结合舰队发展阶段进行规划。高价值蓝图或皮肤往往需要多赛季积累，而紫币等通用资源更适合短期需求。玩家需明确自身定位——侧重PVP强度、收藏或资源储备，从而制定差异化的积分使用策略。这种资源管理机制既增加了游戏深度，也为不同参与度的玩家提供了可持续的目标导向。